After learning x2 and x10 multiplication facts, the next step for students is developing mastery of the 5 times table, or x5 facts.  These are another of the foundational facts, as x5 facts can be used to build x6 (5+1), x7 (5+2), x8 (5+3) and x9 (5+4) facts.  The x5 facts are taught in Level C of MathFactLab's multiplication & division facts program.

The x5 multiplication facts will certainly take students more effort than the previous two levels, but there are many strategies available to help students develop fluency with these facts.  Students using MathFactLab will see the 5 times table represented with beads, area models, dice, clocks and number lines.  For ÷5 facts we use bar diagrams, number lines, and open arrays.

First Step to Learning the 5 Times Table: Skip Counting by Fives

Probably the best way to start working on the x5 multiplication facts is by skip counting.  This allows students to develop familiarity with the multiples of five up to fifty.  Students should already be familiar with skip counting by tens, so skip counting by fives just means adding an extra step, ending with a 5, between each multiple of ten.  

Students will get the rhythm down quickly: alternating between a number ending with a five and a number ending with -ty (with the exception of ten and fifteen).  Five, ten, fifteen, twenty, twenty-five, thirty, thirty-five, etc.  

At MathFactLab, one of our x5 strategies is skip counting, as you can see in the screenshot below.  In our approach, all multiples are listed, with the exception of the multiple required to solve the math fact.  These multiples are placed on a number line.  If the hint button is hit, a marker for each integer is displayed, allowing students to figure out the solution if all other strategies fail.  This is not frequently necessary with x5 facts.

Halving Ten to Find x5 Multiplication Facts

Skip counting is a good starting point for learning the x5 multiplication facts, but not a great final strategy.  To solve 7x5 by skip counting would most likely require seven fingers and counting by five all the way to 35.  We want our students to get to the product much more efficiently than that. 

One way students can get there more quickly is to chop the x10 multiplication facts in half.  For example, 8 tens is 80, so 8 fives will be half of that.   Half of 80 is 40, so 8x5 is 40.  This is faster, avoids fingers, and is based on very easy, previously learned facts.  

At MathFactLab, we teach halving ten with two different models: area and beads.  Both have the same message: take your knowledge of tens to learn the fives.  

 

2 Fives is Ten

Halving ten can be a little trickier for larger, odd multiples of five, such as 7 or 9 fives.  A fair amount of students won't be able to quickly and accurately divide 70 or 90 in half.  For these types of problems, 2 fives is ten is a better strategy.

At MathFactLab, we use dice for this strategy.  For a problem like 7x5, students see seven dice showing five.  These are arranged so students can quickly pair them up, knowing each pair makes ten.  The strategy at the bottom says '2 fives = 10'.  Students can see there are three pairs of fives with one left over: 3 tens plus 1 five = 35.  If needed, the hint button shows the pairs of fives more explicitly.  

 

Clock faces

Clock faces can be another great reinforcer of x5 multiplication facts.  9x5 is rapidly learned if a student knows that when the long hand points to the nine, 45 minutes of the hour have passed.  Of course, in our digital world, a good portion of our students can't read analog clocks very well.  For them, the clock face strategy can actually be used in reverse: Student knowledge of fives can help them to read clocks better.

Division by 5

Of course, we don't only want our students to multiply by five, we want them to also know their ÷5 division facts. And this means facts with either a divisor of 5 or a quotient of 5. For example, 45 ÷ 5 = 9 or 45 ÷ 9 = 5. Both of these are part of the 9, 5, 45 multiplication fact triangle.

With all division facts, the first port of call is to point out to students that they can use multiplication facts to solve division facts, helping them to realize that division is simply 'un-multiplication'. I like to tell my students that if I had been the one to coin math terminology, they would have learned to add and un-add. They would learn to multiply and un-multiply. These terms don't exactly roll off the tongue, but they do help reinforce the connection between inverse operations.

At MathFactLab, our students use open arrays, number lines and bar diagrams to practice and build understanding of the ÷5 division facts. With open arrays, they are explicitly both dividing and finding a missing factor.

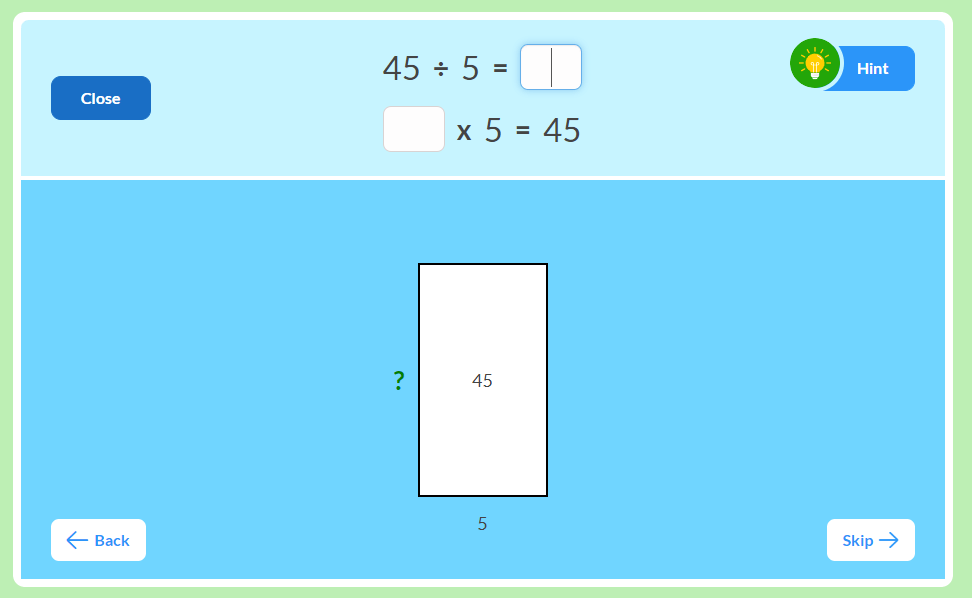
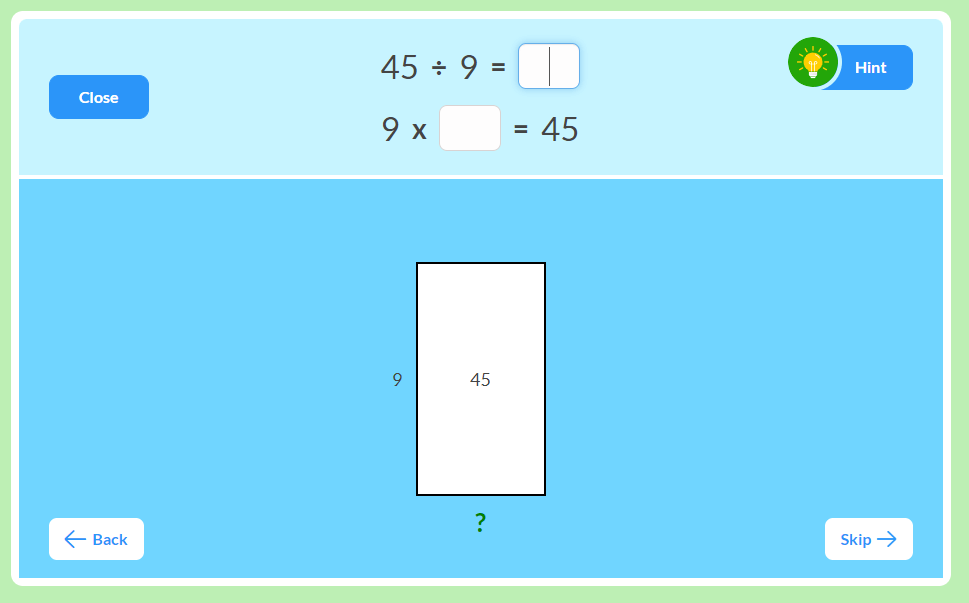
With number lines, students are practicing to quickly find the right multiple of a number given a few landmarks.  In the below example, one hint has been provided.

Of the three, our bar diagrams show division most explicitly.  

 

Conclusion

The x5 multiplication facts need a little more work than the previous two fact groups, but taking them from a multiple model approach - combined with division to reinforce fact-family - thinking should these multiplication facts reasonably achievable.  

MathFactLab provides a similar multi-model, strategic approach for all addition and multiplication fact families.  Learn more here.  

This blog was written by Mike Kenny, 5th grade teacher and creator of MathFactLab.