Math Facts Journal
The blog of MathFactLab
The 4 Times Table: How to Teach x4 Multiplication Facts
Multiplication facts can be mastered without too much difficulty when they are taught using strategies, especially when those strategies build on previously mastered multiplication facts. At MathFactLab, the 4 times table is introduced at Level F, after students have developed proficiency with the x2, x10, x5, x1 and x0 facts. The x4 multiplication facts are the first level of 'derived' facts that students learn, meaning they use foundational facts (x2, x10, x5, x1) to construct them.
Double Doubling to Construct the 4 Times Table
The doubling of x2 facts is the foundation for x4 multiplication facts fluency. Doubling 2 fours (8) to find 4 fours (16) is not much of a problem for kinds. Nor is doubling 2 sevens (14) to find 4 sevens (28). But solving 4x8 and 4x9 can be a little trickier as it requires mentally carrying/regrouping. 16 + 16 is quite a bit more difficult for young students to solve than a problem like 12 + 12.
While 4x9 is introduced at Level F, it is not assessed because doubling 18 is not a particularly efficient strategy. Better ones for this fact are taught at Level J (x9).
MathFactLab models double doubling two ways: with dice and with ten frames, allowing students two ways to visualize this method.
Other Strategies for x4 Multiplication Facts
Skip Counting
Skip counting by fours is not as intuitive as it is for two, tens and fives, but it's still certainly a worthwhile exercise. Some students might pick up on the pattern in the ones digit: 4, 8, 2, 6 , 0, 4, 8, 2, 6, 0, etc.
Area Models
Area models are also helpful for those learning the 4 times table. Students can see the double doubling within the area model by simply bisecting the rectangle to form two 2 x _ rectangles.
Division Strategies for the 4 Times Table
Open Arrays for x4 Division Facts
MathFactLab's open arrays are a great way to help students recognize that division facts and multiplication facts are two sides of the same coin. Students see an open array with the area and one dimension labeled. The other is labeled with a question mark. Students learn that division can be thought of as finding the missing dimension of a rectangle or the missing factor in a multiplication equation.
Bar Diagram Division
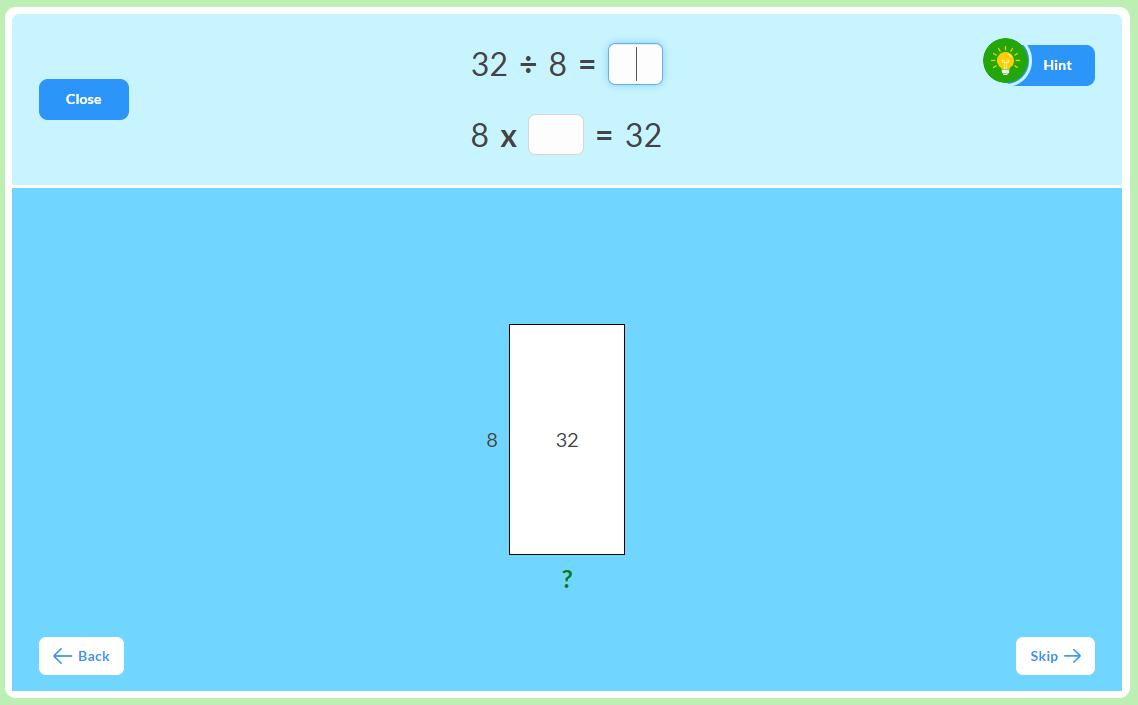
This represents division in perhaps the most straightforward approach. A bar equal to a given quantity is divided into a certain number of pieces. What is the value of each piece.
With this model, students will need to fluently divide by 4 and the other factor making up the fact triangle. For example, students will need to solve both 28 ÷ 7 and 28 ÷ 4.
Number Line Division
Using MathFactLab's number line division, students are asked to think more linearly about the x4 multiplication facts. For example, when solving 32 ÷ 4, students use the anchors of 5 fours and 10 fours to figure out how many fours make 32.
Conclusion
The x4 multiplication facts are the first of the derived facts and certainly need some practice to master, but as the 4 times table is built on the first set of the foundational facts (x2), these facts are not particularly tricky, with the exception of 4x8 and 4x9.