Math fact fluency and math fact automaticity are often used interchangeably by educators, but it's worth understanding the difference between the two.

When I was three, I could sing Frere Jacques in French.  Perhaps, I even sounded almost as good as a little French boy or girl would doing the same.  The difference, however, was that those little French preschoolers most likely understood the words, whereas I didn't have what the song was about.  I had simply memorized sounds; there was no understanding behind my recitation: I didn't know it was about a sleeping brother or morning bells.  I certainly couldn't have changed the words to make it about a laughing sister instead.  

Likewise, two students, when asked the product of 9 and 6, could both reply accurately right away.  We can say that they both demonstrated automaticity (easy recall) with this fact.  If you probe a little deeper, however, Student A might tell you that he knows it's 54 because he memorized his nines.  Probe deeper and you get nothing more.

Student B, on the other hand, might explain that she knows it's 54 because it's 1 six less than 60 and it's double 27.  

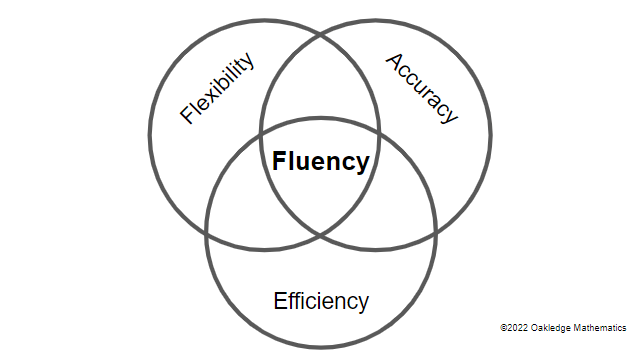
Because both students could respond with little effort, we can say that they demonstrate automaticity with this fact, but student B can also be described as fluent with the fact.  Automaticity is just answering accurately and quickly.  Fluency, is much deeper: It's not necessarily effortless, but it is efficient, flexible and accurate.  

If a student is fluent in their facts they can quickly correct themselves if they make a mistake.  Such a student would realize that 6 x 9 couldn't be 53 because multiples of an even number (such as 6) are even (not like 53).  They would know it's not 52 because it's not 9 more than 45.  But if student A misremembers or one day can't remember, he's stuck.  He's been taught to rely on memory rather than reasoning.  

Students with math fact fluency can apply their fact knowledge to new situations.  If 9 x 6 = 54, they would understand that 9 x 12 could be found by doubling 54.

While we'd ideally like our students to eventually have immediate recall of all the basic math facts, what's more important is the path they take to get there.  If math fact knowledge is developed as part of the process of building deep conceptual understanding.  Such a foundation will serve them whether or not memory immediately can.  

At MathFactLab, our primary goal is to help students develop math fact fluency.  We do this by providing students with multiple models and multiple strategies to tackle any basic math fact.   If you haven't done so already, give us a try.