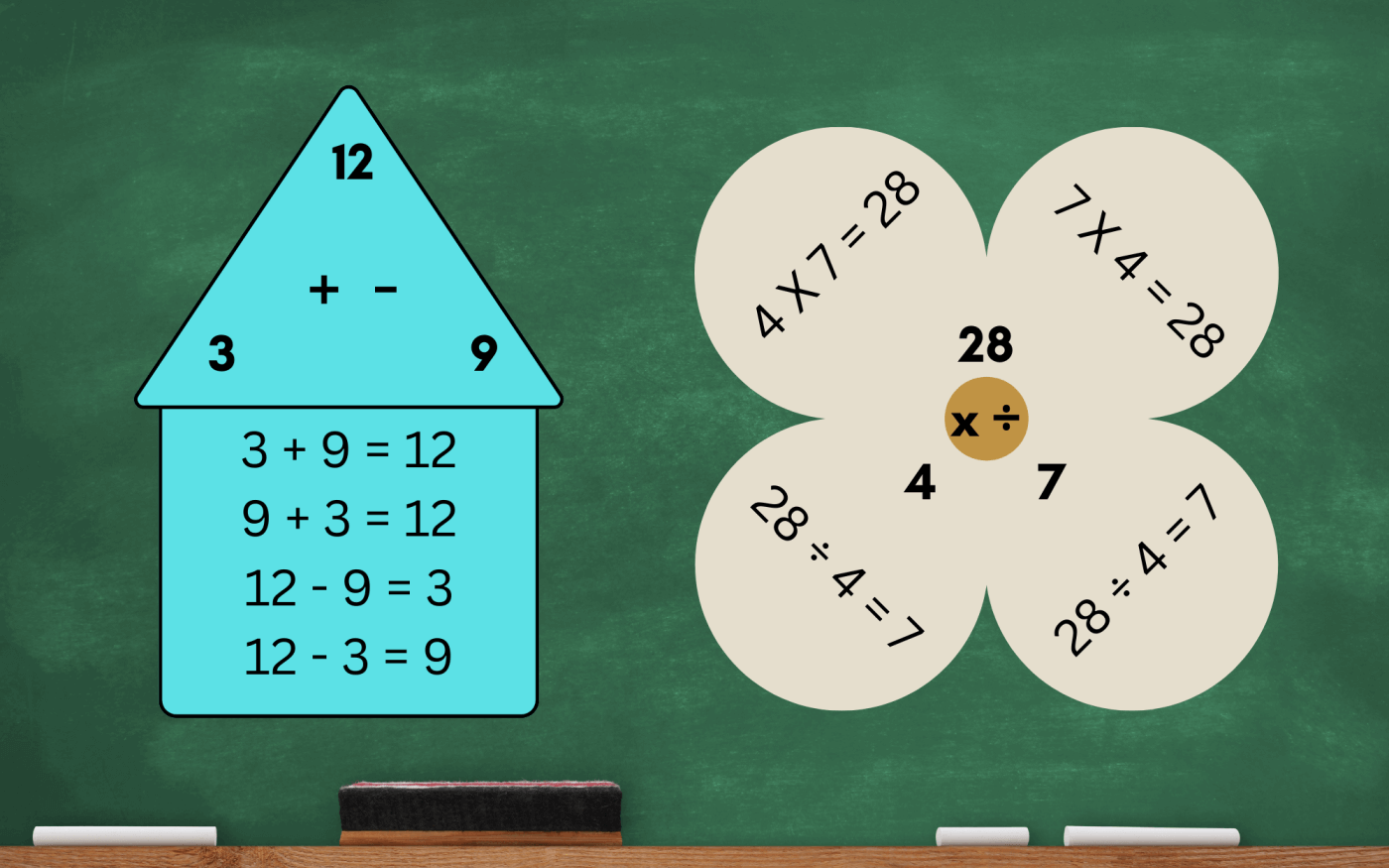
When it comes to teaching math, there are a lot of different methods and strategies that teachers can use to help their students understand concepts and develop fluency. One important strategy that is often used is teaching students to think in terms of math fact families. So, what exactly is a math fact family, and why is it important? Let's take a closer look.

What is a Math Fact Family?

A math fact family is a set of basic fact equations that can be composed with three numbers. Typically, a math fact family will be composed of 4 facts, using 3 numbers. Fact families are constructed with a pair of inverse operations, either addition/subtraction or multiplication/division.

The exception is when we are adding doubles or multiplying the same factor. In these cases, the family is composed of just two related facts.

Addition and Subtraction Fact Families with Examples

An addition and subtraction fact family is built using two addends and their sum.  With these three numbers, we can form (typically) 2 addition equations and 2 subtraction equations.  For example, with the set 3, 4 and 7, we can create the following set of related basic math facts:

• 3 + 4 = 7
• 4 + 3 = 7
• 7 - 4 = 3
• 7 - 3 = 4

The atypical case is when the addends are the same, as in the case of doubles.  When this is the case, we can form only 2 equations.  For example, with the set 7, 7, 14, only one addition and one subtraction basic fact can be created: 

• 7 + 7 = 14
• 14 - 7 = 7

Multiplication and Division Fact Families with Examples

A multiplication and division fact family works similarly.  The building blocks of the fact family are two factors and their product.  This set of three numbers (typically) forms four equations: 2 multiplication and 2 division.  For example, the set 3, 8, & 24 create the following fact family:  

• 3 x 8 = 24
• 8 x 3 = 24
• 24 ÷ 8 = 3
• 24 ÷ 3 = 8

The atypical case for multiplication fact families is when both factors are the same, such as with the set 7, 7, 49.  With such a set, we can only create one multiplication and one division fact, as you can see in the example below:

• 7 x 7  = 49
• 49 ÷ 7 = 7

Math Fact Family Triangles

The three numbers which compose a fact family are often depicted as 'fact family triangles' where one number from the set is placed in each of the three corners.  The pair of inverse operations (addition/subtraction or multiplication/division) is often displayed in the center of the triangle.  

Sample Addition/Subtraction Fact Triangles

In an addition/subtraction fact triangle, the two addends are typically placed in the bottom vertices of the triangle while the sum is placed at the top.  Thinking subtraction, the top number is the minuend (the number we are subtracting from).  Either number can be the subtrahend (the number that is subtracted from the minuend) while the other will be the difference (the result when we subtract). 

Below are example fact triangles from Level G (Near doubles) in MathFactLab's addition/subtraction program.  

Sample Addition/Subtraction Fact Triangles

Sample Multiplication/Division Fact Family Triangles

In a multiplication/division fact triangle, the two factors sit in the bottom corners while the product is placed the top.  In terms of division, the dividend (the number being divided) is at the top.  Either of the numbers at the bottom is the divisor (the number the dividend is being divided by) while the other is the quotient (the result when we divide). 

Below are example multiplication/division fact triangles from Level J (x9) of MathFactLab's multiplication and division program.  

Sample Multiplication/Division Fact Triangles

Math Fact Triangle Crafts Ideas

There are lots of crafty ways you can help your students build a better understanding of math fact families. 

• Fact family houses with triangular roofs.   
• Fact family flowers 
• Fact triangles with popsicle sticks
• Fact family kites with tails
• Fact family ice cream cones
• Fact family origami 
• Fact family butterflies
• Fact family turkeys

Clearly, the possibilities here are virtually endless.  

Why Teach the Basic Math Facts in Terms of Fact Families?

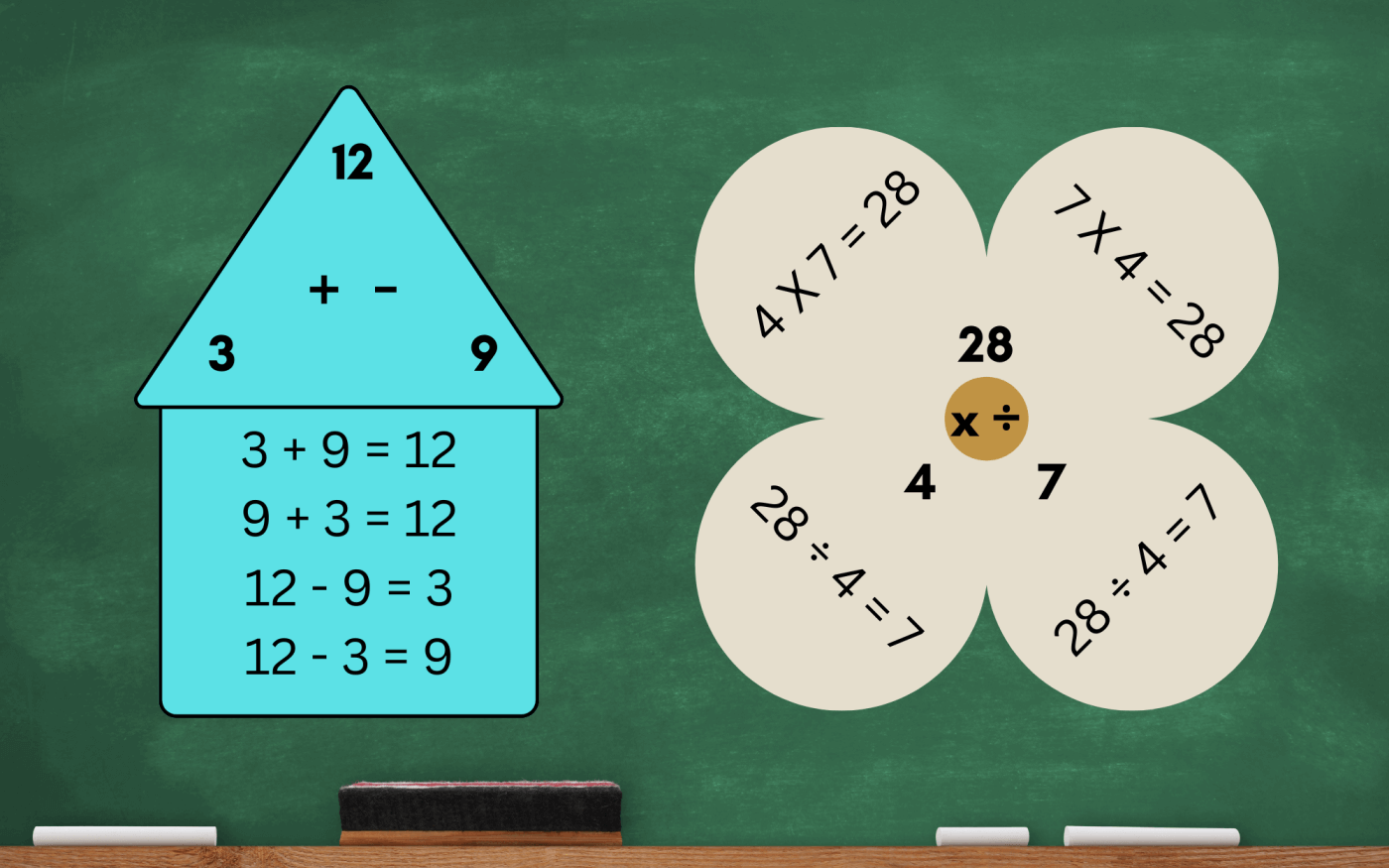
For students, math fact families can be a gateway to greater mathematical understanding. Greater understanding makes learning more efficient and rewarding. As we will explore in the sections below, math fact triangles build a foundation of the commutative property. Understanding commutativity reduces the number of basic math facts (equations with single-digit numbers) that need to be learned in half. Understanding the relationship of inverse math operations makes learning subtraction and division facts simply a matter of reversing equations.

1. Understanding of the Commutative Property

• To review, the commutative property of addition: means that a + b = b + a; order does not matter in addition.  For example, 7 + 4 = 4 + 7.  Sufficient experience with this property through practice will give students the confidence to say that 107,248 + 34,986 must equal 34,986 + 107,248 without feeling the need to actually do any adding.  
• The commutative property of multiplication is similar: a x b = b x a.  Like with addition, order does not matter in multiplication.  For example, 7 x 4 = 4 x 7.  Like with commutativity in addition, when a student sees time and again that order does not matter when working with the basic multiplication facts, they will feel confident in knowing that 8 x 7 can be considered as either 7 eights or 8 sevens, whichever happens to be easier for them to solve.  

Recognition of both of these commutative properties almost cuts the number of math facts in half that need to be learned.  Students don't have to learn both 6 + 8 and 8 + 6; learning one means learning the other.  The same, of course, would be true for 6 x 8 and 8 x 6. 

For teachers, it might be hard for us to imagine not knowing this, but imagine how much more predictable the world suddenly becomes for students when they develop understanding and confidence in the commutative properties.  

2. Increased Understanding of the Inverse Relationship between Operations

When students see that they can make four equations with just the three numbers composing a math fact family, it helps them recognize that addition and subtraction (or multiplication and division) are opposite operations: one undoes the other.  

A proportion of my new fifth graders arrive each year with a fair amount of trepidation about division.  With sufficient practice, they suddenly recognize that "Oh, it's just multiplication backwards!"  At this point, division becomes far less scary.  It also means that they can suddenly use their multiplication fact knowledge to solve division facts.  

I like to tell my students that if I had invented math language, we wouldn't use the words 'subtraction' or 'division'.  Instead, we would use 'un-addition' and 'un-multiplication'.  Why?  Because that's really what subtraction and division are.  Some students take a long time to see that if they can solve 8 + 5 easily, then 13 - 8 is also easily solvable, but once they do, math becomes so much simpler. 

Thinking in terms of fact families helps foster the mathematical understanding that one property of operations is that they have an inverse operation.  The result: Students build number sense and math fact learning gets simplified.  

3. Easier Learning of the Basic Math Facts

In all, counting all four math operations, there are close to 500 basic math facts that students are expected to develop fluency with.  Consider how bewilderingly daunting it would be to be expected to have to memorize 500 facts. 

When students learn to commutativity, that huge number gets cut almost in half.  When students understand inverse operations that number gets cut by about half again.  Thinking (and teaching) with math fact families in mind reduces the task by almost three fourth!  (From there, of course, a range of math fact strategies will dramatically reduce that number further.) 

Conclusion

Why teach your students to see math facts as part of math fact families? In simplest terms, fact families provide a valuable foundation for understanding mathematics. As they help to build a deeper understanding of math facts, fact triangles make the learning of math facts easier.

That fact that the basic facts all belong to fact families can be seen as a pattern. As math teachers, one goal of ours goal is to help our students recognize patterns. The late professor of math education, John Van de Walle, described mathematics as, “The science of pattern and order.”

That the basic math facts do not exist in isolation, but rather as members of families of related facts is one such important pattern our students should be guided toward recognizing. Each time we recognize a pattern, the world makes a little more sense and is a little easier to predict. In mathematics, with each new pattern we learn, our understanding of math becomes broader.

When students know that any addition fact will have a related subtraction fact or two, the learning of one leads to the rapid learning of the other(s). My fifth-grade students often, at the beginning of the year, tell me that they can't do division. I tend to smile at them and say, 'Oh, yes you can.' We look together at the inverse relationship between multiplication and division; this helps them see that division is just, 'un-multiplication' and, presto, they suddenly realize just how much division they already know. Likewise, when a student knows one fact in a math fact family, they suddenly know the others as well.

At MathFactLab, helping our students to think in terms of math fact families is one of our foundational principles.

Further Examples of Math Fact Families

Examples of Addition/Subtraction Fact Families

Examples of Multiplication/Division Fact Families

About MathFactLab

MathFactLab is a teacher-created math fact fluency website.  Using models such as ten frames, number lines, dice, area models, and bar diagrams, MathFactLab teaches math facts in a way that makes sense and builds number sense.  

This blog was written by Mike Kenny, fifth-grade math teacher and creator of MathFactLab.