Math Facts Journal
The blog of MathFactLab
The 6 Times Table: How to Teach x6 Multiplication Facts
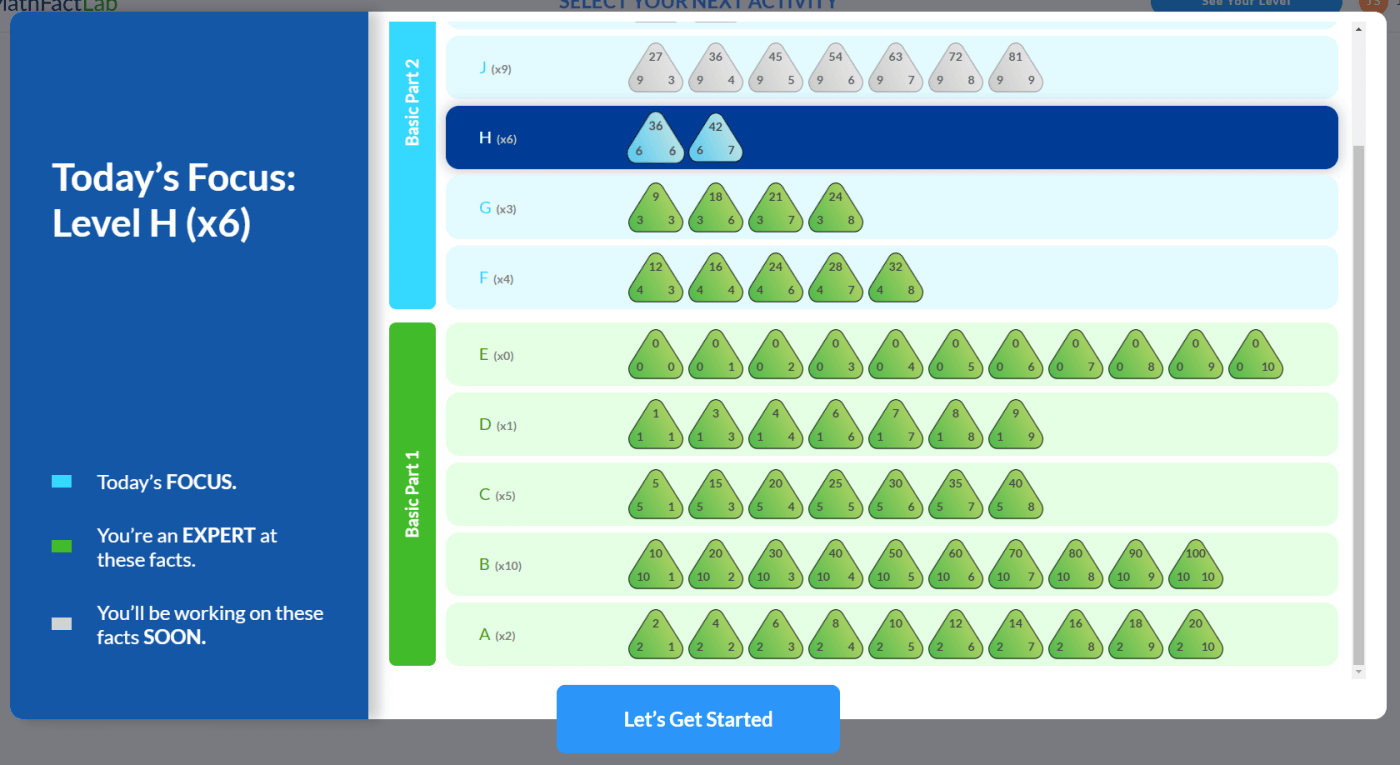
Do you need ideas or strategies for helping your students develop multiplication fact fluency? This is the sixth blog in this series on teaching the multiplication facts, and in it, I'll be covering strategies for helping your students learn the 6 times table. So far, in this series, we have covered several multiplication tables: 2s, 10s, 5s, 4s and 3s.
MathFactLab's multiplication and division math fact fluency program is based on the belief that the basic math facts are most effectively learned when students are able to practice using a variety of strategies and models for each fact. Students learn using a math fact family approach: subtraction facts are taught alongside addition facts and division facts are taught alongside multiplication facts. With this approach, students learn to see the facts as math fact triangles. We provide online math fact practice that meets the needs of virtually all learners.
Foundational Skills for Learning the 6 Times Table
Besides fluency with addition facts, students need to have mastered their 5s and 3s to be successful in learning the x6 multiplication facts. This is because they will be needed to help students build these new facts in two different ways: double 3 groups and 5 groups + 1 group.
Double Three: 6 Groups = 3 Groups + 3 Groups
The simplest approach to teaching the x6 facts is to teach your students to double the x3 facts. For example, if students know that 3x4=12, they can double it to find 6x4. Likewise, doubling 3 sevens helps students quickly solve what can be a difficult fact: 6x7. This doubling method is also very helpful for 6x8 - just double 3x8.
The double 3 method is less helpful for 6x5, 6x6 and 6x9. 6x5 is better solved using fives. 6x6 and 6x9 are more easily solved using 5 groups + 1 group.
6 Groups = 5 Groups + 1 Group
The other main approach to the 6 times table is to harness the power of five. As fives are a foundational fact and tend to be easy to learn, it's a good idea to encourage students to consider fives as an option when building derived facts. By just adding one more group, students have solved for six groups.
To solve for x6, teach students to take five groups and add one more. For example, 6 sixes is 5 sixes (30) plus 1 six (6), giving you 36. This strategy is also particularly helpful with 6x3 (15+3), 6x5 (25+5), and 6x9 (45+9).
Other Strategies for x6 Multiplication Fact Practice
Number Lines
While skip counting is not a particularly effective strategy with sixes, it is still good for students to see all of the sixes on a number line. Take one away, and students should have many approaches to figure out the value of the missing six: Subtract six, add six, or use one of the previous strategies.
Area Models
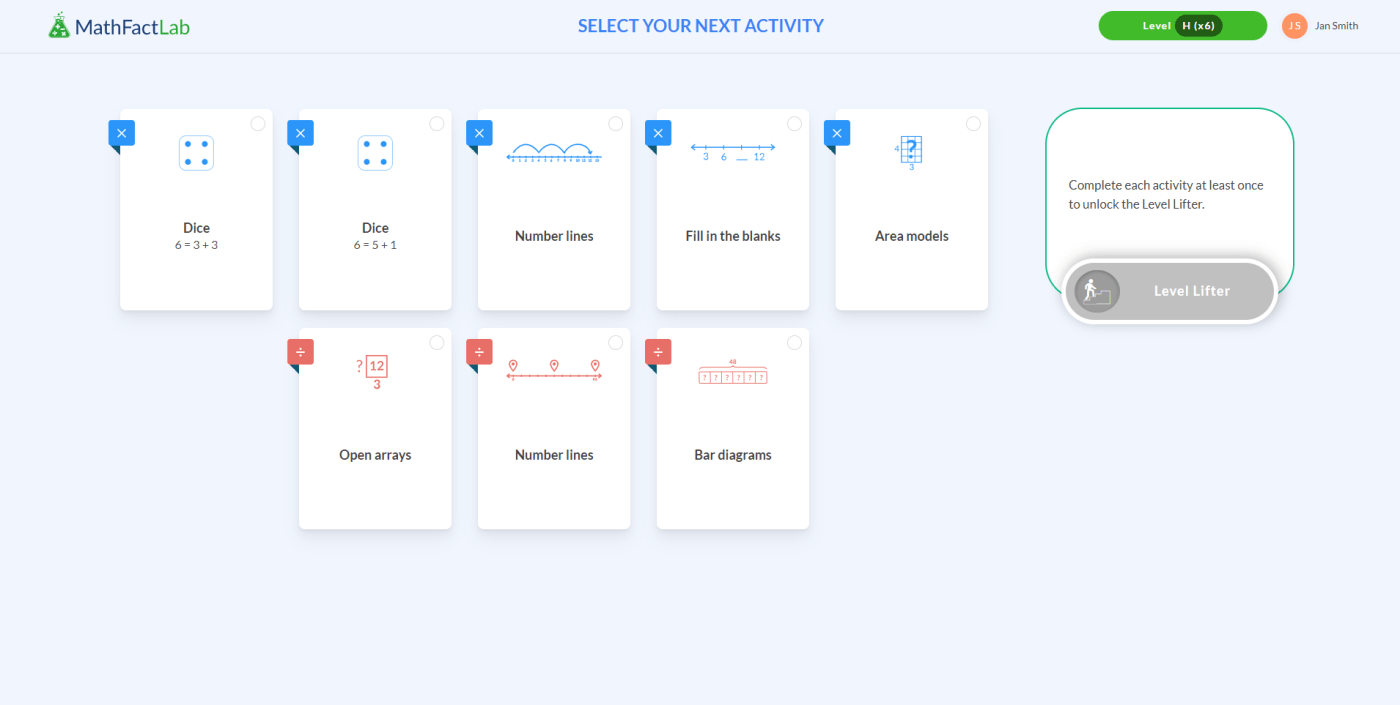
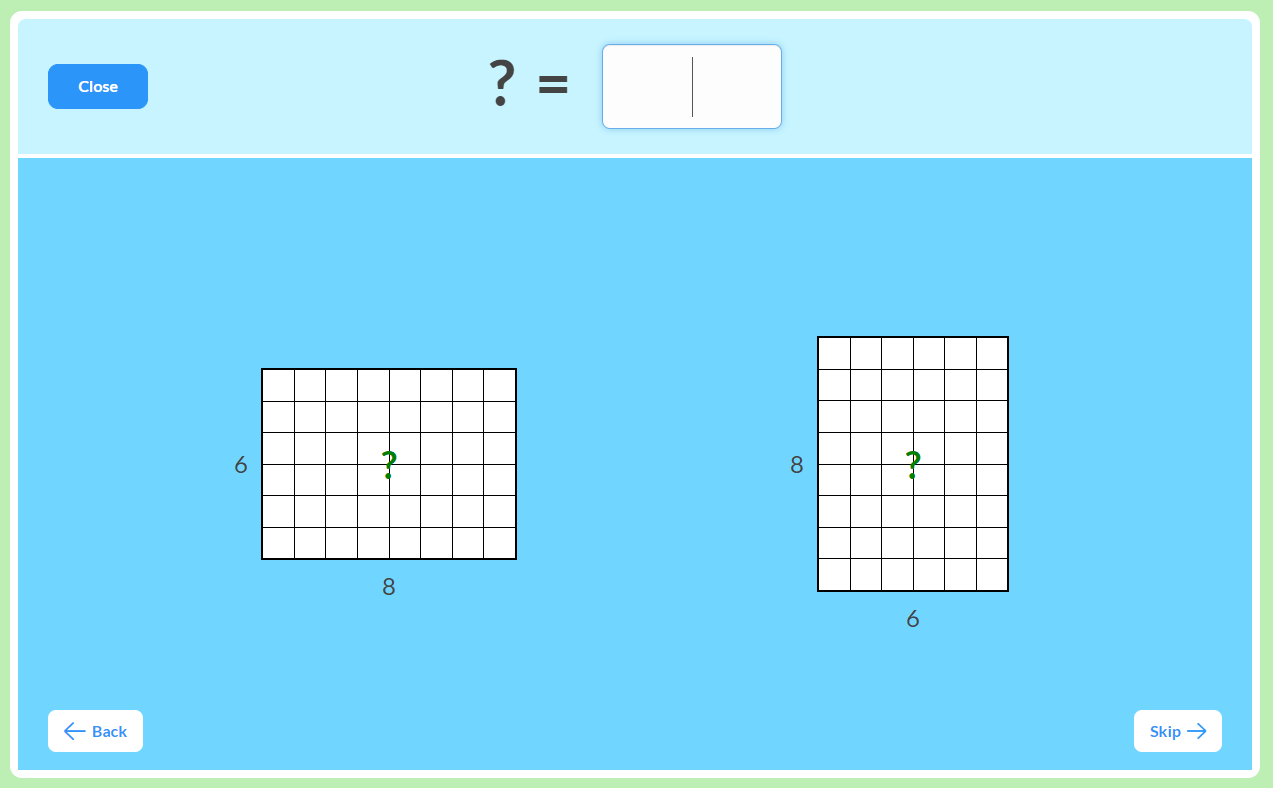
One of the essential models for understanding multiplication (and for learning the basic multiplication facts) is the area model. In MathFactLab's approach, students see area models presented in two ways - vertically and horizontally.
No multiplication equation is listed at the top. Instead, students just see a question mark. This question mark represents the area of either of these rectangles, reinforcing the commutative property of multiplication.
Open Arrays for Division
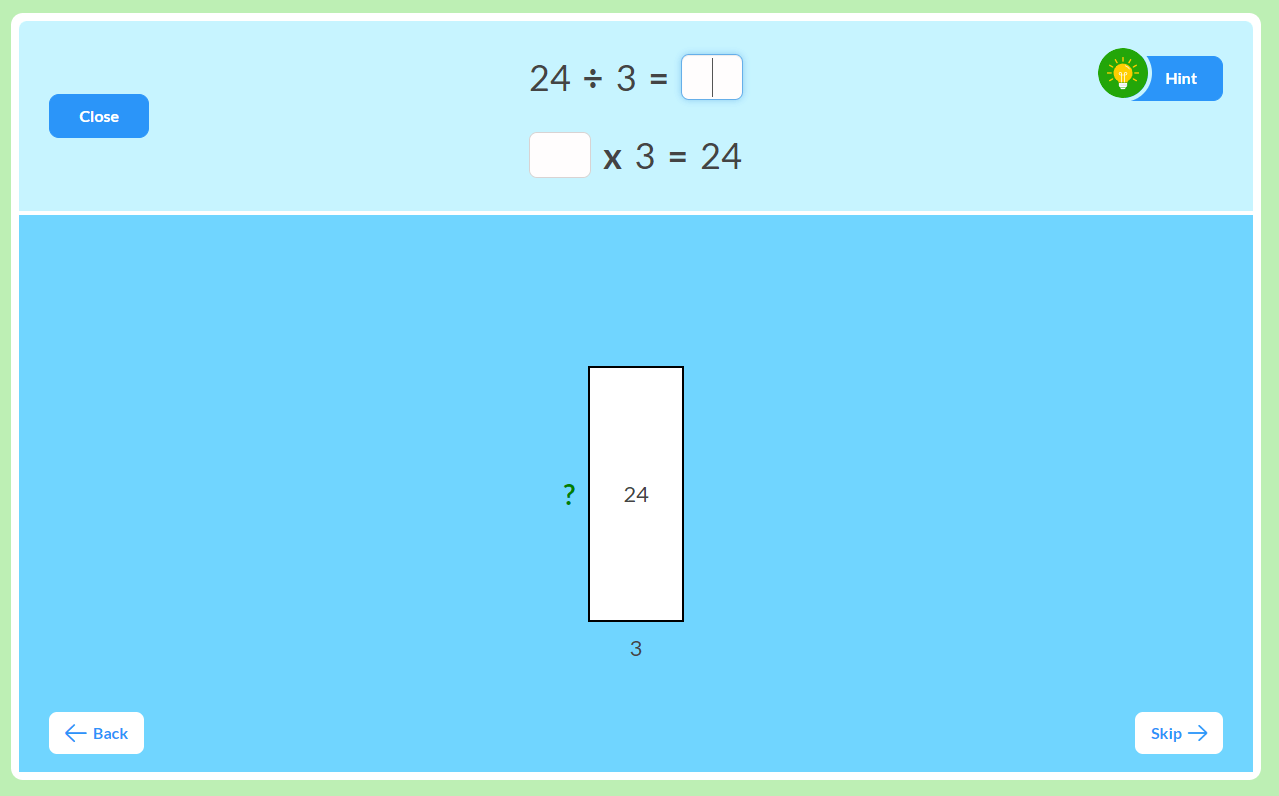
If we provide the area of a rectangle and replace one of the dimensions with a question mark, we have a good model for division. This approach helps students to see that division can be seen as solving for a missing factor.
As the problems are presented both as division (24 ÷ 6 = __ ) and missing factor multiplication ( 6 x __ = 24), students realize that when they are practicing their division facts, they are also practicing multiplication facts.
Bar Diagram Division
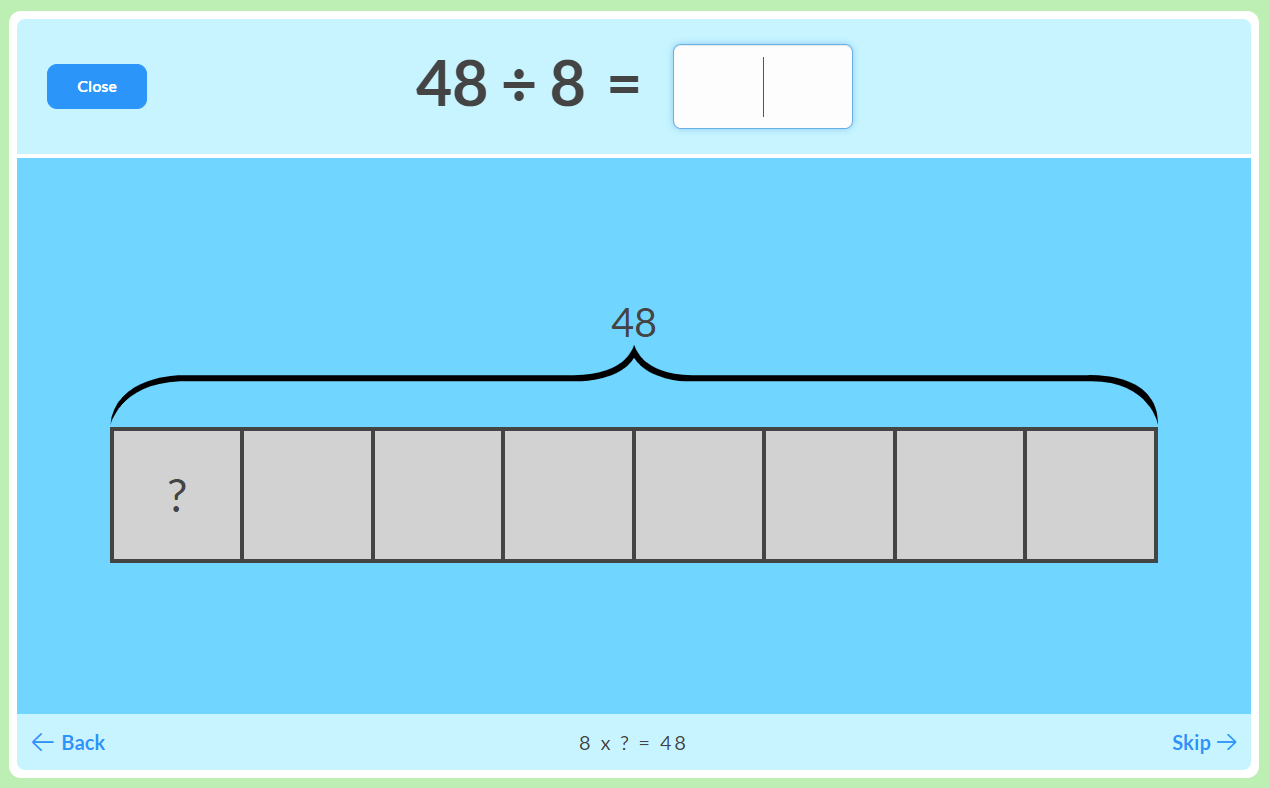
Bar diagrams really help to simplify mathematical concepts. If a bar represents 48, when we cut it into 6 equal pieces we are demonstrating division. Division tends to be more of a stumbling block for kids than any of the other three operations. But when they see it presented in such a simple format, they begin to realize that it's not so complicated. Rather, it's just a means of practicing un-multiplication.
Of course, we could also divide that bar of 48 into 8 pieces, giving students a chance to apply the other factor in the multiplication fact triangle.
Conclusion
While two of the most difficult of the basic multiplication facts are in the 6 times table - 6x7 and 6x8 - with the right mix of strategies, these basic facts too can be learned with relatively little difficulty. By providing your students with a range of methods for approaching the x6 multiplication facts, you are giving them multiple routes to the same destination. If one path happens to be blocked, they will now know another way to get there.
With sufficient math fact practice using the right strategies and models, students will build fluency, and these strategies will be so internalized that they eventually become automatic.
About MathFactLab
Created by a fifth grade teacher, MathFactLab takes a math fact family approach to the basic math facts to help students develop true math fact fluency. When students see addition and subtraction or multiplication and division as actually two sides of the same coin, the amount of facts that they need to learn suddenly shrinks.
Instead of learning hundreds of isolated facts, they instead are learning a few dozen related math fact families, or math fact triangles. Instead of four multiplication and division facts (e.g., 3x4, 4x3, 12÷4, and 12÷3), students learn just one multiplication and division fact family (3 - 4 - 12). This builds student confidence in their own reasoning abilities and in the fact that mathematics is a sense-making, pattern-hunting discipline. One that can be enjoyable for all.
MathFactLab offers individualized, online math fact practice that is strategy-based. Students practice with a range of models for each of the math facts, allowing them to conceive and construct them in a variety of ways. We teach math facts in a way that makes sense and builds number sense.